
オイラーの多面体定理について調べた
普通科3年の田浦君のレポートを紹介します。

まず,オイラーの多面体とは,簡単に説明すると,多面体には頂点,辺,面があり,(頂点の数)-(辺の数)+(面の数)を計算します。すなわち頂点(Vertex)の数を v,辺(Edge)の数を e,面(Face)の数を fとすると,v-e+f=2が成り立つというものです。これを確かめるためにいろんな多面体を書いて調べてみました。
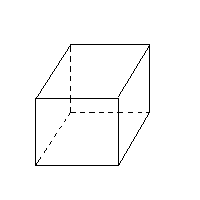 |
<正六面体> v=8 e=12 f=6 v-e+f =8-12+6=2 成り立つ |
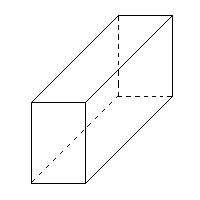 |
<六面体> v=8 e=12 f=6 v-e+f =8-12+6=2 成り立つ |
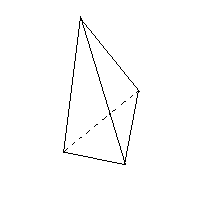 |
<三角すい> v=4 e=6 f=4 v-e+f =4-6+4=2 成り立つ |
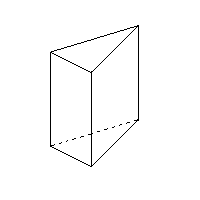 |
<三角柱> v=6 e=9 f=5 v-e+f =6-9+5=2 成り立つ |
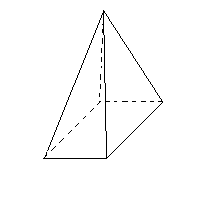 |
<四角すい> v=5 e=8 f=5 v-e+f =5-8+5=2 成り立つ |
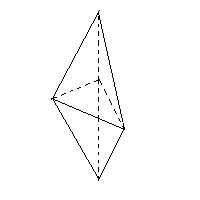 |
<六面体> v=5 e=9 f=6 v-e+f =5-9+6=2 成り立つ |
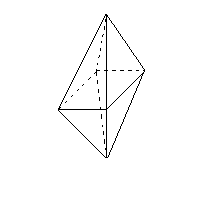 |
<八面体> v=6 e=12 f=8 v-e+f =6-12+8=2 成り立つ |
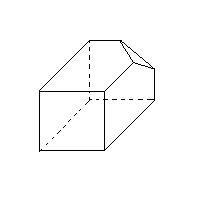 |
<六面体の 一部切り取り> v=10 e=15 f=7 v-e+f =10-15+7=2 成り立つ |
調べてみた結果,正六面体,六面体,八面体,三角柱,三角すい,四角すい,六面体の斜線部を切り取った図形はすべて v-e+f=2 が成り立ちました。他にも多面体はたくさんあるがすべて成り立ちます。
これは,やってみれば分かります。円柱や球も考えたのですが,これは成り立ちません。曲面の入っているものは多面体から除きます。つまり,ここでいう多面体とは平面で囲まれた立体と定義します。
例えば、六面体の頂点のように,3平面で囲まれた頂点を平面で切り取った多面体の頂点,辺,面はそれぞれ,(3-1),3,1 だけ増加するので,切り取ることによって増加した分の v-e+f の値は(3-1)-3+1=0です。すなわち,切り取った多面体における v-e+f の値は変化せず,v-e+f=2 のままです。
同様に,4平面で囲まれた頂点を切り取ると,v-e+f の値の変化量も (4-1)-4+1=0 となり,変化せず,v-e+f =2 です。
一般的に,n平面で囲まれた頂点を切り取ると,v-e+f の値の変化量は (n-1)-n+1=0 で,多面体を何度平面で切り取っても v-e+f=2 が成り立ちます。
以上のように,すべての多面体において v-e+f=2 というオイラーの多面体定理が成り立ちます。
| レオンハルト オイラー(Leonhard Euler, 1707.4.15-1783.9.18). スイスのバーゼルに生まれ,ロシアのサンクト・ペテルブルグに死す。オイラーは当時最高の数学者であったベルヌーイにその才能を見いだされる。カルヴァン派の牧師であった父親は自分の跡を継がせたがったが,ベルヌーイに説得されオイラーが数学者の道を進む事を認めた。20歳の時ペテルスブルグ王立学士院に職を得て,以後死ぬまでここから給料をもらい続ける。 1766年に全盲となるが,死ぬまで活発な研究を続ける。朴とつな人柄で,子供は13人。赤ん坊を抱え,子供を足元で遊ばせながら研究したと言われている。天王星の軌道計算の途中,孫を呼びにやり,お茶を飲みながら話をしている時,突然「死ぬよ」と周りに告げ,穏やかに「生きることと,計算すること」を止めたとも。 ケーニヒスブルクの橋を一筆書きする問題とか,グラフ理論やトポロジーの祖としても。現在数学で使われているπ,Σ(シグマ),∫(インテグラル),sin,cos,log といった多くの記号もオイラーが使ったことから一般的に。 |
| 感想: 僕はこのオイラー多面体定理を調べてみて,日頃何も考えず,日常生活の中にある多面体を見たり,使ったりしていたけど,多面体にこのような共通点があることを初めて知りおどろきました。この多面体定理のように,日常生活で様々なことを意識して考えておれば,もっとおもしろい発見もできそうだと思いました。オイラーの熱心さ,一途さには感心するばかりだが,学ぶことも多い。 |