実は，前ページの２つの問題は，両方とも不可能なんです。
「なあーんだ！馬鹿にしないでよ！」
怒らないで下さい。これから，その理由を考えてみましょう。
「ケーニヒスベルク７つの橋」の問題を不可能だと証明したのが，ドイツの大数学者オイラーです。
１７３６年のことです。
このときの問題解決の発想が，その後，新しい幾何学「トポロジー（位相幾何学）」の誕生のきっかけにもなったのです。
この橋渡りの問題を，「一筆書き」の問題になおして，不可能を証明したのです。
橋を渡る問題を一筆書きの問題と同じだと気づくなんて，やっぱし天才ですね。
一筆書きは，「線がつながっているか」が重要で，途中の線が曲がっていようが，線が短いとか長いかは関係ないのです。
これが「つながりの具合を示す幾何学」である「トポロジー」へと発展するのです。
それでは，「一筆書き」について考えてみましょう。
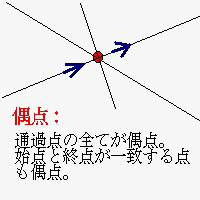
一筆書きには，書き始めの点（始点）と書き終わりの点（終点）があります。それ以外の点（通過点）には，「入る線」があったら，必ず「出る線」がありますので，通過点に集まる線は偶数です。説明を簡単にするために，ある点に集まる線の数が偶数のとき，その点を「偶点」，集まる線の数が奇数のとき「奇点」と呼ぶことにします。
通過点は必ず偶点ですから，始点と終点が一致している場合，その点も偶点（その点は通過点に，書き始めの線と書き終わりの線の２つが加わるから）です。よって，始点と終点が一致するときは，全ての点が偶点です。この場合は，どの点を始点としてもよく，終点を始点と一致させるように書けば良いのです。
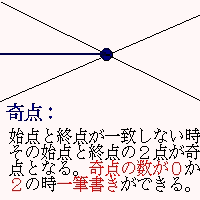
始点と終点が一致しないときは，始点と終点だけが奇点（偶点＋１）で，他は全て通過点で偶点ですから，奇点は２つだけです。この場合は，奇点の片方を始点とし，もう一方の奇点を終点とすればいいのです。
奇点は始点と終点にしかならないので，「一筆書きができる図形は，奇点の数が０個か２個」という結論になります。即ち，一筆書きができるかどうかは，奇点の数を数えればいいのです。
| 奇点が０個の場合 | どの点から出発してもよく，最後に出発した点に戻るようにすればよい |
| 奇点が２個の場合 | 奇点の片方を出発し，最後にもう一方の奇点に戻るようにすればよい |
| 奇点が２個を超える | 一筆書きは不可能 |
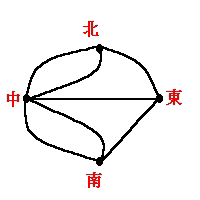
大阪の道頓堀やケーニヒスベルクの問題を，一筆書きの問題（左図はケーニヒスベルクの例で，橋を線で，中の島や各区を点で表した。道頓堀のほうは自分で書いてみて下さい。）として考えれば，一筆書きが不可能だということが解ります。ケーニヒスベルクの場合は奇点が４つ，道頓堀の問題では６つもあり，できないのは当たり前ですね。
「やっぱりできなかったのか，自分もできなかったんだから，それで正解だったんだ！」と思っている人はいませんか。
しかし，それだけでは，正解とは言えません。「できなかった」ことと，「できないことを証明した」というのとは違います。問題には，「できない」とか「解がない」などの解答もあります。その場合は「できない」とか「答えがない」ということを証明しなければなりません。
オイラーが不可能だと証明できたのは，問題の本質をつかみ，単純化（抽象化）に成功したからです。この問題を解くには，橋や島の形や大きさは関係ない，「島（点」）と島（点）が幾つの橋（何本の線）によってつながっているのか！」がポイントだと気付いたからでしょう。不必要な情報や条件に振り回されないこと，情報の取捨選択を的確にすばやく行うことが大切でしょう。情報過多時代を迎え，不要な情報に惑わされることが多い現代社会，学ぶべき点は更に多いかと思っています。
ところで，道頓堀とケーニヒスベルクの２つの問題には，約１００年の差があります。「鎖国状態の江戸時代，ヨーロッパの数学の問題が遠く離れた日本まで，どのような経緯で伝わってきたのでしょうか？」これも，興味ある問題ですね。調べられたり，知っておられる方がいらっしゃったら教えて下さい。
さあ，これであなたも「一筆書きの天才？」となったはずです。
難しい一筆書きの問題は，奇点を２つ，偶点をたくさん持った図形ですね。いろいろ作って，試してみて下さい。